What is compound interest?
Compound interest is arguably the most important concept in finance. Think of it as the ‘snowball’ effect – the concept that capital re-invested will grow at an ever-increasing absolute rate.
Compound interest can be defined as the interest generated from an investment plus all of the interest generated from the interest that has accumulated over time.
The tables below illustrate how the effect of compound interest can have a significant impact after a short period of time. In the first table, annual interest payments received are not reinvested resulting in interest payments remaining static across the three years. However, in the second table, interest payments are invested and so the level of interest increases. By year 3, reinvesting interest payments has resulted in an additional £101 interest payment.
| 7% interest not reinvested | Year 1 | Year 2 | Year 3 |
|---|---|---|---|
| Principal at start of year | £10,000 | £10,000 | £10,000 |
| Interest in year | £700 | £700 | £700 |
| 7% interest reinvested | Year 1 | Year 2 | Year 3 |
|---|---|---|---|
| Principal at start of year | £10,000 | £10,600 | £11,236 |
| Interest in year | £700 | £749 | £801 |
The effect of compound interest becomes even more noticeable over longer periods of time as the amount of accumulated interest grows larger and larger.
How is compound interest calculated?
Compound Interest Formula
The compound interest formula is:
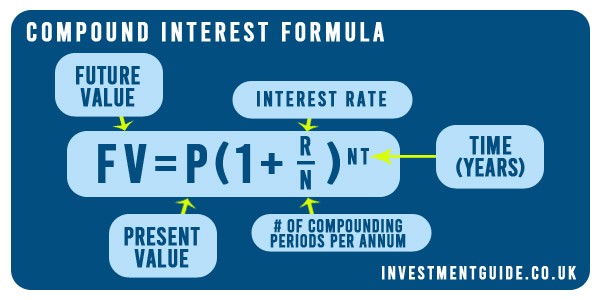
Where:
- FV = Future value
- P = Present value (i.e. your initial principal/investment)
- R = The annual interest/return rate
- N = The number of compounding periods per annum
- T = Number of years
Calculating compound interest in Excel
To calculate compound interest in Excel, you can use the fair value formula:
=FV(rate,nper,pmt,pv)
- Rate – To get the period rate, take the interest rate (e.g. 5%) and divide by the number of compounding periods per year.
- nper – To get the number of periods, multiply the number of compounding periods by the number of years.
- pmt – Number of period payments.
- pv – Enter ‘-presentvalue’. For example, if your starting investment is £10,000, you would enter ‘-10000’.
For example, the below formula calculates the future value of a £10,000 investment in 20 years time assuming a 6% interest rate and 12 compounding periods per annum.
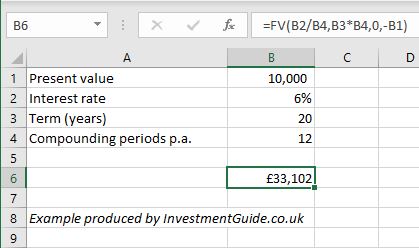
=FV(B2/B4,B3*B4,0,-B1)
=FV(0.06/12,12*20,0,-10000)
=FV(0.005,240,0,-10000)
=33102.04
The Rule of 72 – calculating compound interest in your head
The ‘Rule of 72’ is an interesting way to calculate an approximation for the % return is required to double your money in a certain number of years, given annual compounding.
It’s not perfect, but it derives a good approximation.
So how does it work?
In order to find the number of years required to double your money at a given interest rate, simply divide the interest rate into 72.
For example:
| Rule of 72 | Exact answer | |
|---|---|---|
| 2% | 72/2 = 36.00 | 35.00 |
| 3% | 72/3 = 24.00 | 23.45 |
| 4% | 72/4 = 18.00 | 17.67 |
| 5% | 72/5 = 14.40 | 14.21 |
| 6% | 72/6 = 12.00 | 11.90 |
| 7% | 72/7 = 10.29 | 10.24 |
| 8% | 72/8 = 9.00 | 9.01 |
| 9% | 72/9 = 8.00 | 8.04 |
| 10% | 72/10 = 7.20 | 7.27 |
The calculation also works in reverse. For example, if you want to calculate the interest rate required to double your money in 8 years, you would divide 72 by 8 to calculate an interest rate requirement of approximately 9%.
Why is compound interest an important concept when making savings and investment decisions?
When allocating capital to investment opportunities, it’s important to consider the potential return on investment. Small differences in ROI might not seem like much when thinking about one year in isolation, but over a 20 year period, small % differences can have a material impact.
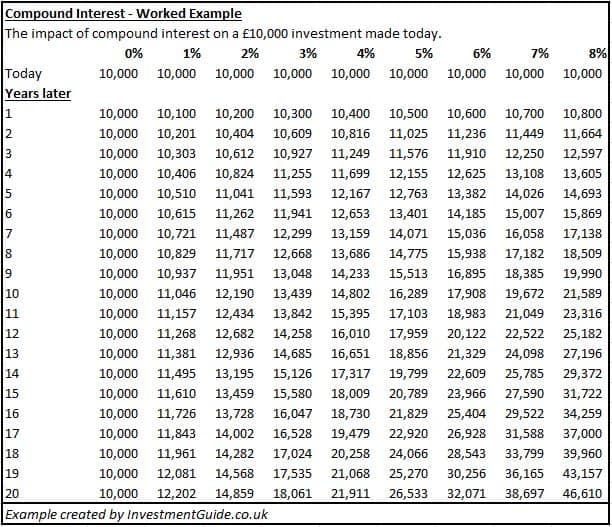
The below table shows how an initial £10,000 investment will grow at interest rates ranging from 0 to 8%, with the calculation assuming that interest is compounded annually.
It shows that a £10,000 investment returning 6% for 20 years will be worth £32,071 whereas an investment returning 1% will be worth just £12,202. This could perhaps represent the difference between investing in a diversified portfolio of shares vs. holding cash in a bank savings account. Remember though, money in 20 years time will be worth less than it is today due to the impact of inflation.
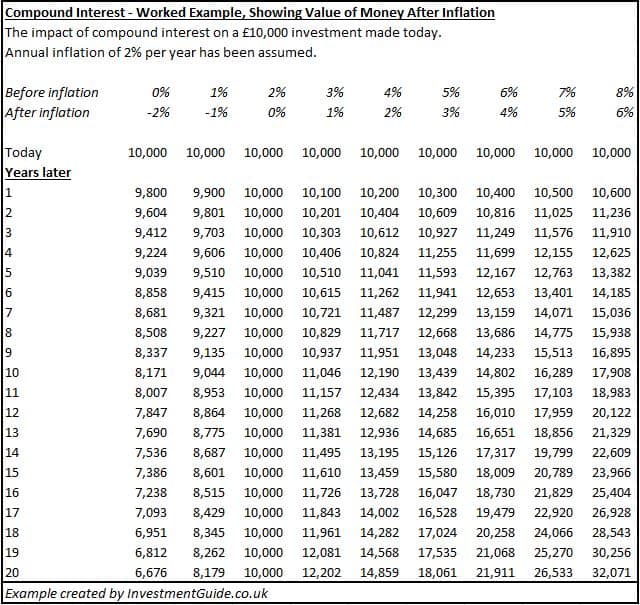
If we assume an inflation rate of 2%, we see that our savings generating 1% interest will actually lose value over time because of inflation. The real equivalent value of our initial £10,000 would in fact decrease to £8,179, whereas our capital invested at 6% would have more than doubled, growing to £21,911.
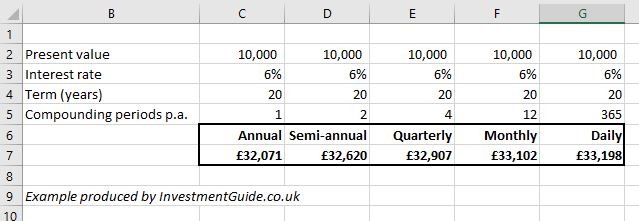
The effect of compounding periods
Interest is commonly compounded daily, monthly, quarterly, semi-annually or annually. However, interest can be compounded on any frequency schedule.
The number of compounding periods can make a big difference to the level of accumulated interest. However, as the frequency of compounding increases, there are diminishing returns.
For example, the below calculation shows that over a 20 year period, interest compounding at 6% would return £549 more semi-annually than it would annually. However, daily compounding interest would only return £578 more than semi-annual compounding interest.